Rafael A. Rosales

Processos Estocásticos

Avaliação Final

A seguinte lista contem as questões que cada um de vocês deve resolver e entregar até o 20/12/2020. Não vou responder dúvidas relativas a própria resolução --só aquelas que tenham a ver com o enunciado. Vou aceitar pdf (podem ser fotos das respostas ecritas a mão) e/ou .txt. Identifiquem o subject no cabeçado do e-mail como "Avaliacao Final". Não vou considerar respostas nos formatos .doc, .docx.

O Jupiterweb entre outras informações fornece o conteudo desta disciplina.

aulas a distância

As aulas serão realizadas pelo Google meet. Vocês devem receber um convite da videoaula ou um link da aula gravada. Penso disponibilizar as aulas durante o semestre tudo para vocês poderem ver varias vezes. Todas as mensagens e convites relativas as aulas serão enviadas ao email de cada um de vocés cadastrado no Jupiterweb (usualmente @usp.br). Qualquer duvida ou sugestão deve ser enviada ao email

duvidas.processos.2020@gmail.com

Não vou responder nehuma mensagem enviada ao meul email @usp.br; a mesma será tratada como spam.

Notas de Aula, Exercícios, Gabaritos

As aulas estão baseadas nas seguintes notas de aula. Estas notas incluem tanto a teoria quanto as listas de exercícios. Qualquer observação, correção ou comentários sobre o conteúdo deste material são bem-vindos.

Eventualmente serão disponibilizados gabaritos para alguns dos exercícios das notas de aula neste site.

Avaliação

Serão colocados vários exercícios ao longo do semestre. Além dos exercícios também estou pensando entregar um ou dois problemas mais avanzados a cada um de vocês. Estes ultimos devem ser respondidos em uma monografia no final do semestre. A monografia terá maior peso na nota final.

Notas

As notas serão postadas no JupiterWeb.

Bibliografía

James Norris. Markov chains. Cambridge University Press. BCRP: 519.217 N856m
Olle Häggström. Finite Markov chains and algorithmic applications. BCRP: 519.217 H145f
Gregory Lawler. Introduction to stochastic processes. BCRP: 519.6 L418i
Geoffrey Grimmett, David R. Stirzaker. Probability and random processes. Oxford University Press. BCRP: 519.21 G864p3.

25/08/20

aula 1

O código em R para as simulações apresentadas na primeira aula se encontra em aula1.R. Um exemplo de como utilizar este script desde R para os processos do "sapo" e da "ruina do jogador" é

  source("http://dcm.ffclrp.usp.br/~rrosales/aulas/aula1.R")
  sapo(p=1)
  sapo(p=0.5)
  sapo(p=0.5, N=200)
  sapoejacare()
  ruina()
  ruina(x0=25)
  ruina(x0=25, seed1=2, seed2=37, seed3=101, N=500)

O resultado da terceira linha é apresentado pelo grafico abaixo.

15/09/20

processo de nascimento/morte simples

O script nasmort.R simula a evolução do número de indivíduos de uma população segundo o processo de nascimento e morte simples descrito em aula. As simulações podem ser geradas desde R da seguinte forma

 source("html://dcm.fflcrp.usp.br/~rrosales/aulas/nasmort.R")
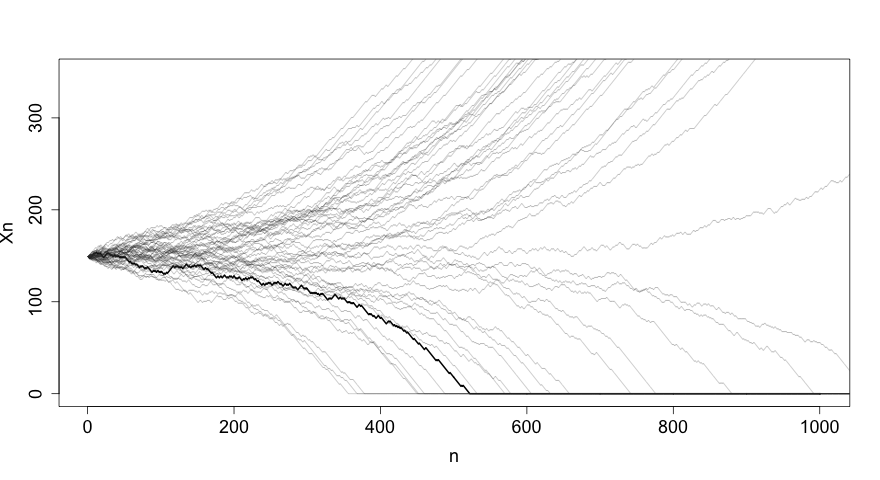
 for (i in 1:50) nasmort(init=150,N=1000, n=1500, pltone=F, pltadd=T)

a função nasmort gera uma trajetória de 1000 passos deste processo; o código acima gera 150 trajetorias. O resultado é apresentado no gráfico abaixo.

6/10/20

passeio aleatório simples em $\mathbb Z^2$

As simulações da trajetória do passeio aleatório simples em $\mathbb Z^2$ podem ser graficadas com o script rw2D.R , por exemplo,

 source("html://dcm.fflcrp.usp.br/~rrosales/aulas/rw2D.R")
 rw2D(n=4000)

A seguinte figura mostra o resultado gerado pelos comandos acima.

20/10/20

simular uma cadeia de Markov ($\mathfrak S$ finito)

A função sample (do R) é a base para simular os valores de uma variável aleatória discreta; por exemplo

  sample(x=c(0, 1), size=1, prob=c(0.5, 0.5))

pode ser utilizado para simular o lancamento de uma moeda honesta, "0" corresponde a coroa e "1" a cara, por exemplo, e

  sample(x=c(0, 1), size=100, prob=c(1/3, 2/3), replace=TRUE)

100 lancamentos de uma moeda com probabilidade de cara 1/3. Analogamente, 200 lancamentos de um dado honesto podem ser simulados da seguinte forma

  sample(c(1,2,3,4,5,6), size=200, prob=c(rep(1/6, 6)) replace=TRUE)

Segundo o explicado em aula, uma cadeia de Markov pode ser simulada utilizando sample. O script markov.R de fato implementa estas ideias. O seguinte codigo ilustra como simular a trajetoria de uma cadeia de Markov com matriz de probabilidade de transicao e distribuicao inicial

  source("http://dcm.ffclrp.usp.br/~rrosales/aulas/markov.R")
  caminho <- markov(N=300)
  [1] "matriz de probabilidade (1a fila, 2a fila, ...):"
  1: 0.2 0.8
  3: 0.2 0.8
  [1] "distribuicao inicial"
  1: 0.5 0.5

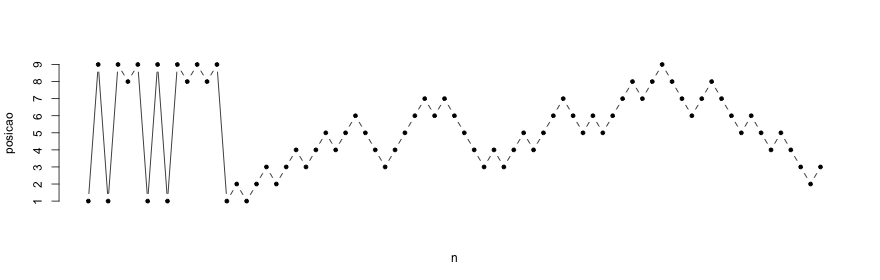
Por de defeito markov grafica a trajetoria simulada. No codigo anterior guardamos a sequencia dos estados vistados pelo processo no objeto caminho. O valor deste objeto pode ser inspecionado simplesmentes digitando

 caminho
  [1] 1 1 2 1 2 2 1 2 2 2 1 1 2 2 2 2 2 2 2 1 2 1 2 2 1 2 2 2 2 2 2 2 1 1 2 2 2
 [38] 1 2 2 2 2 2 2 2 2 2 1 1 2 2 2 2 2 2 1 2 2 1 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2
 [75] 2 2 2 1 1 2 2 2 2 2 2 2 2 2 2 1 1 2 2 2 2 2 2 2 2 1 2 2 2 1 1 2 1 2 2 2 2
[112] 2 2 2 2 1 2 2 2 2 2 2 2 2 1 2 1 2 1 2 1 2 2 2 2 2 2 2 2 1 2 2 2 1 1 2 2 2
[149] 1 2 2 2 2 1 2 2 1 2 2 2 2 2 2 2 2 2 2 1 1 2 2 2 2 2 2 1 2 2 2 2 1 2 2 1 1
[186] 1 1 2 2 2 1 1 2 2 2 2 2 1 2 1 2 2 1 2 2 2 2 2 2 1 1 2 2 2 2 2 2 1 2 2 2 2
[223] 1 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 1 1 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1
[260] 1 2 1 2 2 2 1 2 1 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 1 2 1 2 2 2 2 2 2 2 2
[297] 1 2 2 2 2

o graficado como

plot(caminho, type="b")