Rafael A. Rosales

Introdução a Probabilidade e Estatística II (BCC)

 dados <- read.table("http://dcm.ffclrp.usp.br/~rrosales/aulas/cancer.txt", head=TRUE)

R na sala de aula: simulações, análises, etc

06/03/24

Lei Fraca dos Grandes Números

O script utilizado em sala de aula para simular o lançamento de moedas com probabilidade $p \in [0,1]$ de sair cara e graficar a frequência relativa de caras em $N$ lancamentos pode ser carregado ao digitar

source("https://dcm.ffclrp.usp.br/~rrosales/aulas/moedaWLLN.R")

Este script define a função moedaWLLN(), a qual possui argumentos p, N, m, coins; os quais respectivamente representam a probabilidade $p$, o número de lançamentos, o número de moedas a serem lançadas (cada uma $N$ vezes), e uma variável boleana (com valores TRUE, FALSE) a qual mostra os lançamentps que resultaram em cara e aqueles que resultaram em coroa. Por exemplo

moedaWLLN(p=1/2, N=300, m=1, coins=TRUE)

simula o lançamento de uma moeda honesta 300 vezes e grafica a evolução da frequência relativa de caras $S_n/n$, $S_n = \sum_{i=1}^n \xi_i$, como explicado em aula. Sugiro vocês tentarem varios valores para m e M para ganharem intuição ao que respecta o conceito da convergência em probabilidade inerente na Lei Fraca dos Grandes Números.

17/03/24

Amostras/estimadores 1

Os seguintes comandos tem por objetivo ilustrar a definição de amostras e estimadores.

A função sample pode ser utilizada para gerar amostras de uma população descrita por uma variável aleatória discreta com um número finito de valores. Por exemplo,

sample(x=c(1,2,3,4,5,6), size=300, replace=TRUE, prob=c(2/3,1/15,1/15,1/15,1/15,1/15))

gera a amostra

  [1] 1 1 1 1 3 1 1 1 1 6 6 1 1 1 1 5 1 6 1 6 4 4 1 1 1 1 6 1 1 2 1 1 1 1 1 1 1
 [38] 1 1 3 1 1 3 1 4 1 4 4 1 5 1 1 1 1 5 1 1 4 1 1 1 1 1 3 1 4 1 5 1 1 1 5 1 1
 [75] 1 1 4 1 1 6 1 1 5 2 1 6 1 1 1 1 1 1 1 4 1 3 4 1 1 5 2 4 2 1 1 1 1 2 4 1 1
[112] 2 1 1 1 1 3 4 1 1 1 3 5 5 2 1 1 5 3 4 1 3 1 5 1 2 1 1 1 1 6 2 1 1 1 1 3 5
[149] 1 2 5 1 4 2 4 1 1 1 3 1 4 1 1 1 1 1 4 1 1 2 5 1 1 4 1 1 1 1 1 3 1 1 1 3 3
[186] 1 1 3 1 1 1 4 3 1 3 1 6 1 1 1 4 5 1 1 1 2 4 1 1 1 4 1 6 5 1 1 1 6 1 2 3 1
[223] 5 1 1 4 5 3 1 1 4 1 1 1 5 1 2 1 1 1 1 1 6 6 6 3 4 2 2 1 1 1 1 1 4 1 2 5 1
[260] 1 6 1 1 1 4 4 1 1 1 1 1 6 3 2 3 5 1 4 1 1 1 1 1 3 1 4 1 1 2 4 1 1 1 1 1 4
[297] 2 1 1 1

a qual representa o resultado de termos lançado 300 vezes um dado não honesto, com probabilidade 2/3 de resultar em 1. Para simular 10 lançamentos de uma moeda honesta e de outra com probabilidade 1/4 de resultar em cara podemos fazer (1 representa cara)

sample(x=c(0,1), size=10, replace=TRUE, prob=c(1/2,1/2))
sample(x=c(0,1), size=10, replace=TRUE, prob=c(3/4,1/4))

R posue funções para gerar amostras de uma grande quantidade de distribuições, alguns exemplos são: rnorm, rpois, rgeom, rbinom, rchisq e rt. O seguinte exemplo gera uma amostra de tamanho 200 de uma população Poisson$(\lambda)$ com $\lambda=10$,

rpois(lambda=10, n=200)
   [1] 12 15 11 10 10 12 12  7  7 10 14  6 15 11  9  9  6 14  6  9 15 15  8 13  6
  [26] 13 12 10 11  8 12 11  9 10 10  8  9 13  4  7  9  9 18 13 10 15  8 11  7 10
  [51] 10  9 15  5 10 13  4  7  9 10 10 12  8 12  7 15 14 11  6 14  9  5 12 12 15
  [76] 15 14 12 13 11  7 12  6 10 12  3  8  6 13  5 14  9 12 11 12  6  8  5 11 17
 [101]  3 14 11 12 10 11  6  9  8  8  2  9  6 14 13  7 12 10 10  9  9 11 11  8 10
 [126]  9  5 13 17 13  7  9  5  8 17 13 10 11  8  7  9 10  8  4  8  7  6 11 10 14
 [151] 12 11 15  8 10  8  5  8 12  6 11 10 21  6 11 10  4  8  9 12  7 14 11 11 20
 [176] 10 12 14  6 13 10  8  7  6 17  5  9  5  6  5 10 10 14 15  9  6  9 12  9  8

Suponhamos que a polulação das alturas dos estudantes da USP seja normal com média 1.68 (m) e variância 0.01. A seguinte linha utiliza a função rnorm para gerar uma amostra de tamanho 10 desta população e armacena os valores gerados no vetor alturas,

alturas <- rnorm(n=10, mean=1.68, sd = sqrt(0.01))

Definimos a seguir uma função da amostra, $g(X_1, \ldots, X_n)$, com o objetivo de estimar a média da população (suponha que o valor 1.68 utilizado para gerar a mostra seja realmente um parâmetro desconhecido),

g <- function(x){ 
  print(sum(x)/length(x)) 
}

A função $g$ calcula a media amostral, isto é, para a amostra $X_1, \ldots, X_{10}$, o estatístico $g$ retorna $10^{-1}\sum_{i=1}^{10} X_i$. O resultado ao aplicarmos o estimador na amostra gerada é,

g(alturas)

Podemos gerar mais amostras e observar os valores do estimador em cada uma, por exemplo

for (i in 1:5) g(rnorm(n=10, mean=1.68, sd = sqrt(0.01)))
 [1] 1.706853
 [1] 1.662526
 [1] 1.690708
 [1] 1.688903
 [1] 1.752636

gera 5 amostras e calcula a media amostral de cada uma. Em sala de aula denotamos $g(X_1, \ldots, X_n)$ por $\bar X$, o estimador média amostral. O importante aqui é observarmos como a depender da amostra podem resultar valores diferentes para o estimador $\bar X$: estes valoressão todos estimativas de $\bar X$. Cada chamada a rnorm muda a semente utilizada pelo gerador de números aleatórios utilizados por esta função gerando portanto amostras possívelmente diferentes. Em lugar de g(), definida acima, R possue a função mean. var é o estimador denotado $S^2$, i.e. a variância amostral $S^2 = (n-1)^{-1}\sum_{i=1}^n (X_i -\bar X)^2$, utilizado para estimar a variância da população $\sigma^2$. A raíz quadrada de $S^2$, o desvio padrão da amostra, é implementado no R pela função sd. Assim, para $\sigma = 0.1 = \sqrt{0.01}$, temos

for (i in 1:5) print(sd(rnorm(n=10, mean=1.68, sd = sqrt(0.01))))
 [1] 0.1147967
 [1] 0.1123809
 [1] 0.1028526
 [1] 0.08733143
 [1] 0.1061369

04 e 08/04/24

máxima verosimilhança

  amostra <- rgeom(15, 1/10)
  p.maxver <- length(amostra)/(sum(amostra)+length(amostra))
  LogVerGeom <- function(x=amostra, p=1/2) { 
     length(x)*log(p) + sum(x)*log(1-p)
  }
  p <- seq(0,0.2,0.001)
  plot(p, LogVerGeom(amostra, p))
  abline(v=p.maxver, lty=2)

O código acima fornece um exemplo do método máxima verossimilhança para uma população $X$ com distribuiça;ão Geometrica($p$), $p$=1/10. Suponha que $X$ representa o tempo de espera em um ponto de onibus qualquer em Ribeirão Preto; $p$ representa a probabilidade de pegarmos o onibus em um minuto. Se $p$=1/10, em méia devemos esperar 10 minutos. A primeira linha do código acima gera uma amostra de tamanho 15 da população. R ao contrario do feito em aula parameterisa o modelo Geometrico da seguinte forma \[P(X = k) = (1-p)^k p, \qquad k = 0, 1, \ldots\] Neste caso o estimador de máxima verossimilhança é $\hat{p}_{MV} = n/\sum_i (X_i-1)$, sendo $X_i$, $1 \leq i \leq n$ a amostra de $X$. A primiera linha do código gera uma amostra com $n=15$. A segunda linha calcula a estimativa do estimador $\hat{p}_{MV}$. A terceira linha define a função LogVerGeom, a qual calcula o logaritmo da função de verosimilhançã na amostra, dado um valor para $p$. A quarta linha define um vetor com possíveis valores para $p$. A quinta linha grafica o logaritmo da verosimilhança em funçao de $p$. Por ultimo adicionamos a posição da estimativa para $p$. Esta ultima deveria estar no lugar de máxima verossimilhança. Sugiro voce executar o script acima tal qual e logo substituindo a primeira e a quarta linha por

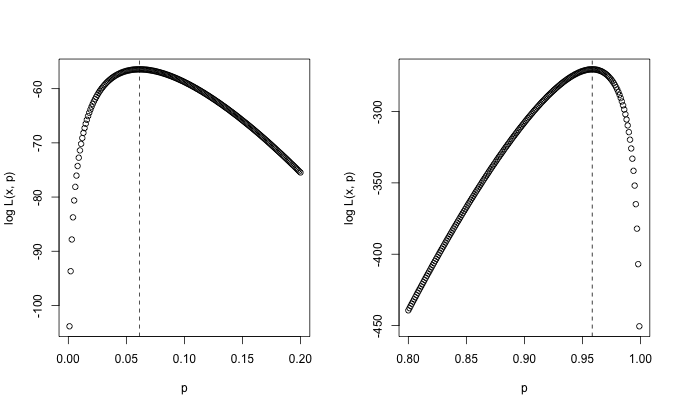
  amostra <- rgeom(1500, 0.95)
  p <- seq(0.8,1,0.001)
  p.maxver <- length(amostra)/(sum(amostra)+length(amostra))
  plot(p, LogVerGeom(amostra, p), xlab="p", ylab="log L(x, p)")
  abline(v=p.maxver, lty=2)

O valor $p$=0.95 poderia ser utilizado para modelar a probabilidade de pegarmos o onibus no primiero minuto na Alemanha, por exemplo. Os graficos gerados pelos comandos acima é apresentado abaixo.

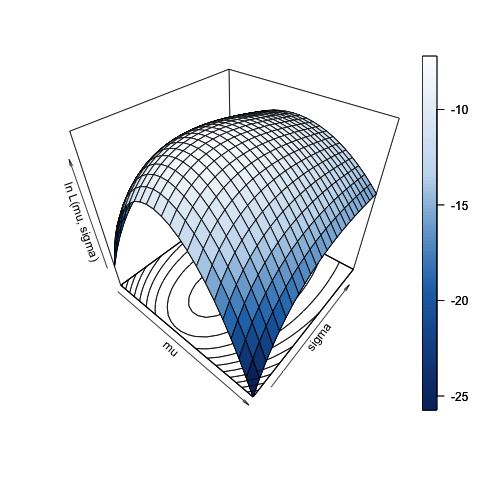
O script NormalLik.R simula uma amostra de tamanho 40 de uma população normal com média 1.68 e variância 0.1 (com o intuito de simular uma amostra das alturas de vocés) e posteriormente calcula e grafica a superficie de verossimilhanca para um determinado dominio dos valores para a média e a variância. O grafico abaixo apresenta o resultado. Tente executar o script várias e observe a variação da superficie determinada pela amostragem! Observe que para poder gerar o grafico, é necessário instalar a livraria plot3D, digitanto, por exemplo, desde a linha de comando do R install.packages("plot3D").

O script também imprime o valor das estimativas para os estimadores de máxima verossimilhança baseados na amostra; veja os numeros impresos na linha de comando que aparecem depois de digitar

source("http://dcm.ffclrp.usp.br/~rrosales/aulas/NormalLik.R")

10/04/24

Distribuição empirica como estimador da funcão de distribuicão da populacão

  source("http://dcm.ffclrp.usp.br/~rrosales/aulas/empirical_pdf.R")
  dado(N=10)
  plotFn(dado(N=10))
  for (i in 1:6) plotFn(dado(N=10), add=T)
  plotFn(dado(N=10000), add=T, col.hor="red", lwd=3)
  # amostras de uma populacao normal padrao (mu=0, sd=1)
  plotFn(normal(N=30), xlim=c(-3,3))
  for (i in 1:3) plotFn(normal(N=30), add=T)
  plotFn(normal(N=15000), add=T, col.hor="blue", lwd=3)
		  

A primeira linha carrega as funções definidas em empirical_pdf.R. A segunda linha gera uma amostra $X_1$, $X_2$, $\ldots$, $X_{10}$, a qual representa o lançamento de um dado honesto 10 vezes. Isto é implementado com a função dado, a qual por sua vez utiliza a função do R sample. A terceira linha calcula e grafica a estimativa para $\widehat F_{n}(x)$ baseada na amostra gerada com dado. A quarta linha calcula e grafica mais outras seis estimativas, cada uma obtida com uma amostra diferente (subsequentes chamadas a sample geram amostras "aleatórias" diferentes; tente você mesmo). A quinta linha calcula e grafica a estimativa obtida com uma amostra de tamanho n=10000, ou seja uma sequência de números obtida ao lançarmos 10000 um dado!. A estimativa desta ultima deve estar bem próxima da função de distribuição de um dado honesto. As ultimas linhas repetem esta experiencia para amostras de uma população normal padrão, isto é, com média 0 e variância 1. Ambos os resultados são mostrados na figura abaixo.

10/04/24

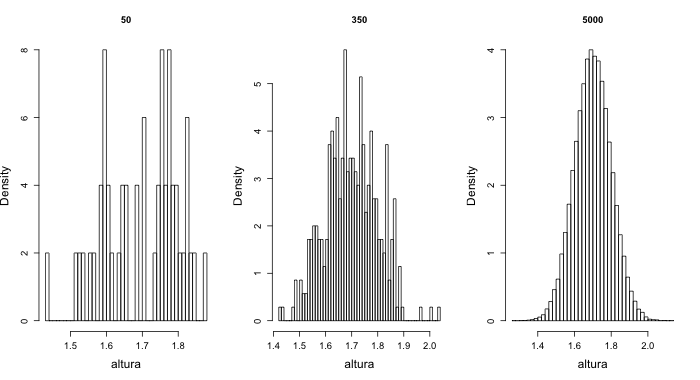
A segunda parte das simulações apresentadas em aula ilustram a convergência (em probabilidade) do histograma $\widehat h_{n}(x)$ a distribuição da população $f$,\[\widehat h_n(x) \underset{\mathbb P}{\longrightarrow} f(x).\] No código abaixo, sala.BCC.* é uma amostra de tamanho *=50, 350, 5000 de uma populacao normal com media 1.7 e desvio padrão 0.1, utilizada para simular a altura de vocês (em metros). Este exemplo não foi realizado na aula, mas queiro disponibilizar aqui para voces terem ainda mais exemplos.

sala.BCC.50 <- rnorm(52, mean=1.7, sd=0.1)
hist(sala.BCC.50, breaks=50, main="50")
sala.BCC.350 <- rnorm(350, mean=1.7, sd=0.1)
hist(sala.BCC.350, breaks=50, main="350")
sala.BCC.50000 <- rnorm(50000, mean=1.7, sd=0.1)
hist(sala.BCC.50000, breaks=50, main="50000")

O resultado é apresentado na figura abaixo.

O seguinte exemplo, feito em aula, ilustra a convergencia do histograma quando a densidade da população segue o modelo Exponencial($\lambda$) com $\lambda=3$

T.50 <- rexp(n=50, rate=3)
hist(T.50, breaks=50, main="50", xlab="tempo")
T.350 <- rexp(n=350, rate=3)
hist(T.350, breaks=50, main="350", xlab="tempo")
T.50000 <- rexp(n=50000, rate=3)
hist(T.50000, breaks=50, main="50000", xlab="tempo")

Neste caso $X$ pode representar o tempo de espera para ser atendido em um posto de saude em minutos ($\lambda = 3$ é o tempo médio de espera).

15/05/24

Testes de hipótese: função poder

O seguinte script do R mostra como calcular a função poder para o exemplo relativo ao teste bilateral para uma proporção $p$ visto em aula correspondente ao problema relativo a proproção de agua salobra em poços artesianos no nordeste. Os valores criticos $x_1 = 0.347$ e $x_2=0.453$ foram calculados ao escolher um nível $\alpha$.

# pa: vetor de valores para o valor da proporcao alternativa isto é o intervalo [0, 1] - 0.4
pa <- seq(0,1,0.001)
x2 <- 0.453
x1 <- 0.347
f2 <- pnorm((x2-pa)/sqrt(pa*(1-pa)/400))
f1 <- pnorm((x1-pa)/sqrt(pa*(1-pa)/400))
poder <- 1 - abs(f2-f1)
plot(pa, poder)
abline(v=0.5, lty=2)

É importante vocês entenderem o que a função pnorm do R representa, e por que ela é utilizada aqui. O grafico resutante é apresentado abaixo.

29/05/24: testes de hipotese no R

Os seguintes exemplos apresentam as respostas a alguns dos exercícios da lista envolvendo teste sde hipótese utilizando R. Em particular são consideradas as funções t.test, var.test e prop.test. Sugiro executar cada um dos comandos descritos abaixo e interpretar os resultados.

Primeiro exemplo: teste t-Student não pareado, Exercicio 71

d <- read.table(file="http://dcm.ffclrp.usp.br/~rrosales/aulas/energy.txt", head=TRUE)
attach(d)
obesas <- subset(d, stature=="obese", select=c(expend))
magras <- subset(d, stature=="lean", select=c(expend))
boxplot(magras, obesas)
boxplot(expend~stature, data=d)
t.test(expend~stature, paired=FALSE)
t.test(obesas, magras, paired=FALSE)

Testes relativos ao Exercicio 74 (inclue uma teste para verificar a igualdade de variancias de duas amostras)

tbr <- read.table(file="http://dcm.ffclrp.usp.br/~rrosales/aulas/trabalho.txt", header=TRUE)
head(tbr)
attach(tbr)
plot(Periodo, Branca, ylim=c(0,80))
points(Periodo, Amarela, pch=19, col="blue")
points(Periodo, Indigena, pch=19, col="red")
points(Periodo, Preta, pch=19, col="magenta")
t.test(Branca, Preta, paired=FALSE)
t.test(Branca, Indigena, paired=FALSE)
t.test(Branca, Preta, paired=FALSE)
var.test(Branca, Preta)
t.test(Branca, Preta, paired=FALSE, var.equal=FALSE)

Exercicio 73 (não feito em aula!)

frangos <- read.table(file="http://dcm.ffclrp.usp.br/~rrosales/aulas/chiken.txt", header=TRUE)
frangos
head(frangos)
frangos[1:3,]
frangos[1:20,]
attach(frangos)
boxplot(weight ~ Diet, xlab="tratamento", ylab="peso (gr)")
t.test(weight ~ Diet, paired=TRUE, alternative="two.sided")
t.test(weight ~ Diet, paired=FALSE, alternative="two.sided")
t.test(weight ~ Diet, paired=FALSE, alternative="less")
t.test(weight ~ Diet, paired=FALSE, alternative="greater")

O resultado é da linha 7 é apresentado na figura a baixo.

Testes para uma proporção. Suponhamos que uma moeda seja lancada 30 vezes e que como resultado tenham sido obtidas 18 caras. O seguinte teste permite verificar se a moeda é honesta (o argumento p=0.5 determina o valor da hipotese nula para a probabilidade de sair cara)

prop.test(18,30,p=0.5)

Suponhamos agora que o resultado dos 30 lancamentos tenham sido 27 caras. O teste

prop.test(27,30,p=0.5)

fornece um $p$-valor extremadamente pequeno, o qual significa que temos evidencia bastante forte para rejeitarmos a hipotese nula $p=0.5$. O seguinte teste para a diferenca de duas proporcoes considera o lancamento de duas moedas 50 vezes, a primeira resulta em 27 caras e a segunda em 35. Por defeito a hipotese nula é $p=0.0$, o qual corresponde a pensarmos que as duas moedas tenham a mesma probabilidade de resultar em cara

prop.test(c(27,35),c(50,50))

05/06/24: regressão linear aplicada a casos de COVID-19 na região de Ribeirão Preto

O seguinte codigo ilustra a analise realizada com os dados covid-RP. Os dados apresentam o número de casos novos de COVID-19 reportados por dia na região de Ribeirão Preto desde o 27/03/21 até 12/07/21 (dados oficiais da Secretaria da Saude; mais detalhes podem ser encontrados no cabeçado do próprio arquivo de dados).

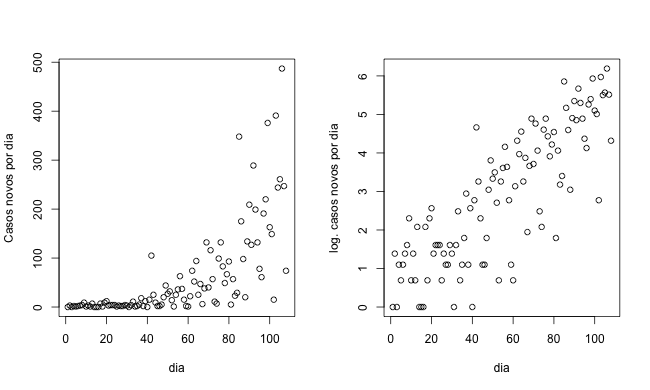
Os seguintes comandos importam os dados e geram um gráfico do numero de casos novos por dia e também um gráfico do logaritmo do numero de casos novos.

dados <- read.table("Covid-RP.txt", head=TRUE)
attach(dados)
help(par) 
op <- par(mfrow = c(1, 2))
plot(dia, Nov, xlab="dia", ylab="Casos novos por dia")
plot(dia, log(Nov+1), xlab="dia", ylab="log. casos novos por dia")

O resultado é apresentado na seguinte figura.

O seguinte script reliza uma regressão linear aos dados transformados logaritmicamente. O comando summary fornece um resumo da analise de regressão; vejam a minha aula para entender o output de summary.

regre <- lm(log(Nov+1) ~ dia)
summary(regre)

Call:
lm(formula = log(Nov + 1) ~ dia)

Residuals:
    Min      1Q  Median      3Q     Max 
-2.4646 -0.5225  0.1721  0.6833  2.3392 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 0.379256   0.187963   2.018   0.0461 *  
dia         0.046309   0.002994  15.469   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.9699 on 106 degrees of freedom
Multiple R-squared:  0.693,     Adjusted R-squared:  0.6901 
F-statistic: 239.3 on 1 and 106 DF,  p-value: < 2.2e-16

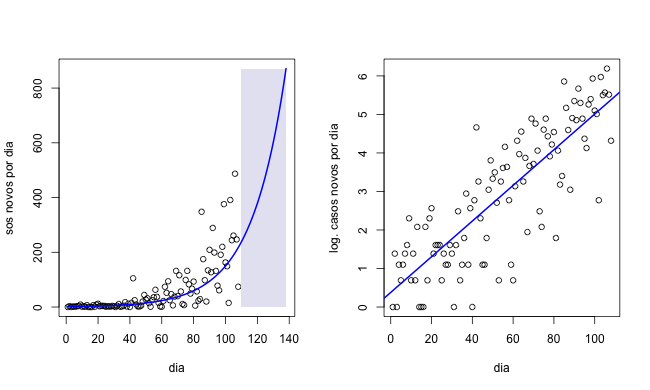
O seguinte código sobrepoe a reta de regressão $y = \hat\beta x + \hat \alpha$ obtida no passo anterior aos dados transformados logaritmicamente e também mostra o grafico da função $e^{\hat\beta x + \hat\alpha}$ sobreposta no dados na escala original.

x <- seq(1,length(dia)+30)
beta <- 0.046309
alpha <- 0.379256
f <- exp(x*beta + alpha)
par(mfrow = c(1,2))
plot(dia, Nov, xlim=c(1,length(dia)+30), ylim=c(0,max(f)), xlab="dia", ylab="Casos novos por dia")
rect(110, 0, 108+30, max(f), col = rgb(0.9,0.9,0.95), border = NA)
lines(x, f, lwd=2, col="blue")
plot(dia, log(Nov+1),xlab="dia", ylab="log. casos novos por dia")
abline(regre, lwd=2, col="blue")

O resultado é apresentado na figura a baixo.

No grafico na escala original é considerada uma projeção do modelo de regressão 30 dias depois do ultimo dado em 12/07 (área achurada em azul). Isto ultimo só faz sentido se supomos que a fase de crescimente exponencial ainda persista nos próximos 30 dias. É bem possível que isto ultimo não seja realista e de fato existem métodos muito mais sofisticados, fora do alcance do nosso curso introdutório, para fazer previsões. De qualquer forma, espero que seja um incentivo para estimular futuros estudos e mostrar que o método de regressão pode ser, quando utilizado corretamente, uma ferramenta poderosa.